HALF-LIFE OF RADIOACTIVE ELEMENTS

Half-life of Radioactive Elements 

Radioactive decay (also known  nuclear decay or radioactivity) is the process by which an unstable atomic nucleus loses energy (in terms of mass in its rest frame) by emitting radiation, such as an alpthingticle, beta particle with neutrino or only a neutrino in the case of electron capture or electron in the case of internal conversion. A material containing such unstable nuclei is considered  radioactive. Certain highly excited short-lived nuclear states can decay through neutron emission, or more rarely, proton emission. Radioactive decay is a stochastic (i.e. random) process at the level of single atoms, in that, according to quantum theory, it is impossible to predict when a particular atom will decay, regardless of how long the atom has existed. However, for a collection of atoms, the collection's expected decay rate is characterized in terms of their measured decay constants or half-lives. This is the basis of radiometric dating. The half-lives of radioactive atoms have no known upper limit, spanning a time range of over 55 orders of magnitude, from nearly instantaneous to far longer than the age of the universe. A radioactive nucleus with zero spin can have no defined orientation, and hence emits the total momentum of its decay products isotropically (all directions and without bias). If there are multiple particles produced during a single decay, as in beta decay, their relativeangular distribution, or spin directions may not be isotropic. Decay products from a nucleus with spin may be distributed non-isotropically with respect to that spin direction, either because of an external influence such as an electromagnetic field, or because the nucleus was produced in a dynamic process that constrained the direction of its spin. Such a parent process could be a previous decay, or a nuclear reaction. The decaying nucleus is called the parent radionuclide (or parent radioisotope), and the process produces at least one daughter nuclide. Except for gamma decay or internal conversion from a nuclear excited state, the decay is a nuclear transmutation resulting in a daughter containing a different number of protons or neutrons (or both). When the number of protons changes, an atom of a different chemical element is created.

The first decay processes to be discovered were alpha decay, beta decay, and gamma decay.

HALF-LIFE 

Half-life Chart 

Half-life (symbol t1⁄2) is the time required for a quantity to reduce to half its initial value. The term is commonly used in nuclear physics to describe how quickly unstable atoms undergo, or how long stable atoms survive, radioactive decay. The term is also used more generally to characterize any type of exponential or non-exponential decay. For example, the medical sciences refer to the biological half-life of drugs and other chemicals in the human body. The converse of half-life is doubling time.
Ernest Rutherford's discovery of the principle 1907:

The original term, half-life period, dating to Ernest Rutherford's discovery of the principle in 1907, was shortened to half-life in the early 1950s. Rutherford applied the principle of a radioactive element's half-life to studies of age determination of rocks by measuring the decay period of radium to lead-206.
Half-life is constant over the lifetime of an exponentially decaying quantity, and it is a characteristic unit for the exponential decay equation. The accompanying table shows the reduction of a quantity as a function of the number of half-lives elapsed.

Probabilistic Nature

Probabilistic Nature of Half-life 

A half-life usually describes the decay of discrete entities, such as radioactive atoms. In that case, it does not work to use the definition that states "half-life is the time required for exactly half of the entities to decay". For example, if there is just one radioactive atom, and its half-life is one second, there will not be "half of an atom" left after one second. Instead, the half-life is defined in terms of probability: "Half-life is the time required for exactly half of the entities to decay on average". In other words, the probability of a radioactive atom decaying within its half-life is 50%.
For example, the image on the right is a simulation of many identical atoms undergoing radioactive decay. Note that after one half-life there are not exactlyone-half of the atoms remaining, only approximately, because of the random variation in the process. Nevertheless, when there are many identical atoms decaying (right boxes), the law of large numbers suggests that it is a very good approximation to say that half of the atoms remain after one half-life.
Law of Large Numbers 

Law of Large Numbers 

The law of large numbers is a principle of probability according to which the frequencies of events with the same likelihood of occurrence even out, given enough trials or instances. As the number of experiments increases, the actual ratio of outcomes will converge on the theoretical, or expected, ratio of outcomes. The law of large numbers is sometimes referred to as the law of averages and generalized, mistakenly, to situations with too few trials or instances to illustrate the law of large numbers. This error in logic is known as the gambler’s fallacy.

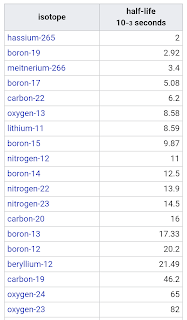
List of Radioactive isotopes by Half-life 

• yoctoseconds
  
• zeptoseconds

attoseconds

Femtoseconds

Picoseconds

Nanoseconds

Microseconds

Milliseconds

            

seconds

kilo seconds

megaseconds

gigaseconds

tetraseconds

petaseconds

exaseconds

zettaseconds

yottaseconds

10 to the power 27 seconds

10 to the power 30 seconds

Why is the half-life of radioactive elements important? 

A knowledge of radioactive half-life is important because
⚫ It enables the dating of artifacts.
⚫ It allows us to calculate how long we must store radioactive waste until they become safe.
⚫ It enables doctors to use safe radioactive tracers.
Half-life is the time it takes for one-half of the atoms of a radioactive material to disintegrate. Scientists can use the half-life of carbon-14 to determine the approximate age of organic objects. They determine how much of the carbon-14 has transformed. They can then calculate the age of a substance.
All nuclear reactors produce radioactive waste. The waste must be stored until it is safe for disposal.
The rule is that a sample is safe after 10 half-lives. Thus, we can dispose of waste containing iodine-131 (t½ = 8 days) after 80 days. We must store the plutonium-239 in spent nuclear fuel (t½ = 24 000 years) for almost a quarter of a million years. Doctors use radioactive isotopes as medical tracers.
The nuclei must be active long enough to treat the condition, but they must also have a short enough half-life so that they don’t have time to injure healthy cells and organs.

Why do scientists measure things by half-life?

Radiocarbon Date Calibration Curve

At the centre of every atom is a dense region called a nucleus, which consists of protons and neutrons. In some atoms, the fforces in the nucleus are balanced and the nucleus has an excess of internal energy; it's unstable, or radioactive.These particles can be detected, typically with a Geiger counter. In the case of radiocarbon dating, a common dating method for organic matter that uses carbon -14 (an isotope, or variant, of the element carbon) to estimate age, one radioactive 'beta particle ' is produced for every carbon -14 atom that decays. By comparing the normal abundance of carbon -14 in a living creature (which is the same concentration in the atmosphere) with the amount left in the material being dated, based on the known decay rate, scientists can figure out roughly how long ago whatever they’re looking at was still alive.
Half-life steps onto the scene in the decay process. While the lifespan of any individual atom is random and unpredictable, the probability of decay is constant. You can't predict when an unstable will break down, but if you have a group of them, you can predict how long it will take. Atoms that have an equal probability of decaying will do so at an exponential rate. That is, the rate of decay will slow in proportion to the amount of radioactive material you have. 

Importance of half-life in Chemistry

Radioactivity 

Scientists look at half-life decay rates of radioactive isotopes to estimate when a particular atom might decay. A useful application of half-lives is radioactive dating. This has to do with figuring out the age of ancient things. 

If you could watch a single atom of a radioactive isotope, U-238, for example, you wouldn’t be able to predict when that particular atom might decay. It might take a millisecond, or it might take a century. There’s simply no way to tell. But if you have a large enough sample, a pattern begins to emerge. It takes a certain amount of time for half the atoms in a sample to decay. It then takes the same amount of time for half the remaining radioactive atoms to decay, and the same amount of time for half of those remaining radioactive atoms to decay, and so on.